Antike Verschlüsselung

Skytale

Die Skytale ist eines der ältesten bekannten Verschlüsselungsverfahren der Geschichte und wurde bereits im 5. Jahrhundert v. Chr. von den Spartanern verwendet, besonders während des Peloponnesischen Krieges.

Wie funktioniert die Skytale?

Die Skytale besteht aus einem Holzstab mit einem bestimmten Durchmesser. Um eine Nachricht zu verschlüsseln:

1. Man wickelt ein langes Band aus Leder oder Pergament um den Stab
2. Man schreibt die Nachricht längs entlang des Stabes
3. Man wickelt das Band wieder ab
4. Das abgewickelte Band zeigt nur wirre Buchstaben

Beispiel:

Wenn man "ANGRIFF UM MITTERNACHT" um einen Stab wickelt und wieder abwickelt, könnte das Band so aussehen:

A I T M G T I R E F N F C U H M T A R N C H

Der Empfänger braucht einen Stab mit genau dem gleichen Durchmesser, um die Nachricht wieder lesbar zu machen.

Besonderheit

Die Skytale ist ein Transpositionsverfahren - die Buchstaben werden nicht verändert, sondern nur ihre Reihenfolge wird durcheinander gebracht.

Schlüsselraum

Der Schlüssel bei der Skytale ist der Durchmesser des Stabes. In der Praxis gibt es nur eine begrenzte Anzahl sinnvoller Durchmesser (ca. 5-20 verschiedene), was einen sehr kleinen Schlüsselraum bedeutet.

Schwäche

Das Problem: Es gibt nur wenige mögliche Stabdurchmesser, die praktisch sind. Ein Angreifer könnte einfach verschiedene Stabdicken ausprobieren, bis die Nachricht lesbar wird.

Polybios

Das Polybios-Quadrat wurde um 150 v. Chr. vom griechischen Historiker Polybios erfunden. Es war ursprünglich nicht für geheime Nachrichten gedacht, sondern für Fernkommunikation mit Fackeln.

Wie funktioniert Polybios?

Die Buchstaben des Alphabets werden in ein 5×5-Quadrat eingetragen. Jeder Buchstabe wird dann durch seine Koordinaten (Zeile, Spalte) ersetzt.

Das Polybios-Quadrat:

	1	2	3	4	5
1	A	B	C	D	E
2	F	G	H	I/J	K
3	L	M	N	O	P
4	Q	R	S	T	U
5	W	X	Y	Z

Hinweis: I und J teilen sich ein Feld, da das lateinische Alphabet 26 Buchstaben hat.

Beispiel:

HALLO  →  23 11 31 31 34
H=23, A=11, L=31, L=31, O=34

Vorteil gegenüber der Skytale

Im Gegensatz zur Skytale werden die Buchstaben hier tatsächlich verändert (in Zahlenpaare umgewandelt), nicht nur umgeordnet. Dies ist ein Substitutionsverfahren.

Schlüsselraum

Das klassische Polybios-Quadrat hat keinen Schlüssel - es ist immer gleich aufgebaut. Der Schlüsselraum ist also 1 (nur eine Möglichkeit). Man könnte das Alphabet im Quadrat durchmischen, aber das wurde ursprünglich nicht gemacht.

Schwäche

Das Polybios-Quadrat allein bietet wenig Sicherheit, da es immer gleich aufgebaut ist. Wenn man das System kennt, kann man jede Nachricht sofort entschlüsseln. Es gibt keinen echten "Schlüssel".

Cäsar

Die Caesar-Verschlüsselung wurde um 100 v. Chr. von Julius Caesar verwendet, um militärische Nachrichten an seine Generäle zu schicken. Laut dem römischen Historiker Sueton benutzte Caesar eine Verschiebung um 3 Stellen.

Wie funktioniert die Caesar-Verschlüsselung?

Jeder Buchstabe im Alphabet wird um eine feste Anzahl von Stellen verschoben. Diese Anzahl ist der Schlüssel.

Beispiel mit Schlüssel 3:

Alphabet:    A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Verschoben:  D E F G H I J K L M N O P Q R S T U V W X Y Z A B C

Klartext:    HALLO
Geheimtext:  KDOOR

Vorteil gegenüber Polybios

Die Caesar-Verschlüsselung hat einen echten Schlüssel (die Verschiebungszahl). Ohne diesen Schlüssel muss ein Angreifer raten oder ausprobieren.

Schlüsselraum

Der Schlüsselraum der Caesar-Verschlüsselung umfasst 25 mögliche Schlüssel (Verschiebungen um 1 bis 25 Stellen). Eine Verschiebung um 0 wäre keine Verschlüsselung, und eine Verschiebung um 26 würde wieder zum Original führen.

Schwäche

Der Schlüsselraum ist sehr klein: Es gibt nur 25 mögliche Verschiebungen (1-25, bei 26 wären wir wieder beim Original). Ein Angreifer kann einfach alle 25 Möglichkeiten durchprobieren (Brute-Force-Angriff) und wird schnell die richtige finden.

Beispiel eines Brute-Force-Angriffs:

Geheimtext: KDOOR
Verschiebung 1: JCNNQ
Verschiebung 2: IBMMP
Verschiebung 3: HALLO  ← lesbar!

Zusätzlich: Jeder Buchstabe wird immer gleich verschlüsselt. Das "L" in HALLO wird beide Male zu "O". Das macht die Verschlüsselung anfällig für weitere Angriffe.

Substitutionsverfahren (Allgemeine Monoalphabetische Substitution)

Um die Schwäche der Caesar-Verschlüsselung zu beheben, kann man ein zufälliges Ersetzungsalphabet verwenden, anstatt nur zu verschieben.

Der allgemeine Fall

Bei der allgemeinen monoalphabetischen Substitution wird jeder Buchstabe durch einen beliebigen anderen Buchstaben ersetzt - nicht nur durch eine feste Verschiebung.

Beispiel eines zufälligen Schlüssels:

Alphabet:       A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Ersetzung:      Q W E R T Y U I O P A S D F G H J K L Z X C V B N M

Klartext:       HALLO
Geheimtext:     IQSSG

Vorteil gegenüber Caesar

Der Schlüsselraum ist enorm groß! Es gibt 26! (26 Fakultät) mögliche Ersetzungsalphabete. Das sind etwa 403.000.000.000.000.000.000.000.000 Möglichkeiten! Ein Brute-Force-Angriff ist damit praktisch unmöglich.

Schlüsselraum

Der Schlüsselraum der allgemeinen monoalphabetischen Substitution beträgt 26! ≈ 403 Septillionen mögliche Schlüssel. Jeder Schlüssel ist eine andere Anordnung des Alphabets.

Vergleich:

• Caesar: 25 mögliche Schlüssel
• Allgemeine Substitution: 403.291.461.126.605.635.584.000.000 mögliche Schlüssel

Das Problem

Trotz des riesigen Schlüsselraums hat diese Verschlüsselung eine entscheidende Schwäche: Jeder Buchstabe wird immer gleich ersetzt. Diese Regelmäßigkeit kann ausgenutzt werden - durch die Häufigkeitsanalyse.

Ausprobieren: Monoalphabetische Verschlüsselung

Monoalphabetische Verschlüsselung

Klartext eingeben:

Häufigkeitsanalyse

Im 9. Jahrhundert entwickelte der arabische Gelehrte Al-Kindi eine geniale Methode, um monoalphabetische Substitutionen zu knacken: die Häufigkeitsanalyse.

Die Grundidee

In jeder Sprache kommen bestimmte Buchstaben häufiger vor als andere. Im Deutschen sind das:

Häufigste Buchstaben im Deutschen:

1. E (≈17%)
2. N (≈10%)
3. I (≈8%)
4. S (≈7%)
5. R (≈7%)

Seltene Buchstaben: Q, X, Y

Wie funktioniert die Häufigkeitsanalyse?

1. Man zählt, welche Buchstaben im Geheimtext am häufigsten vorkommen
2. Man vermutet, dass der häufigste Buchstabe im Geheimtext für "E" steht
3. Der zweithäufigste steht wahrscheinlich für "N"
4. Man probiert diese Zuordnungen aus und verfeinert sie

Beispiel:

Geheimtext: IQSSG VTSG
Häufigkeit: I=1, Q=1, S=3, G=2, V=1, T=1

S kommt am häufigsten vor → S könnte L sein
G kommt zweithäufigsten vor → G könnte O sein

Versuch: I?LL? ?T?O
Ergibt:  HALLO WELT (durch weitere Verfeinerung)

Zusätzliche Hinweise

• Doppelbuchstaben im Deutschen: LL, SS, EE, NN, MM
• Häufige Wortenden: -EN, -ER, -CH, -TE
• Kurze Wörter: "der", "die", "das", "und", "ein"

Warum funktioniert das?

Die monoalphabetische Substitution ändert zwar die Buchstaben, aber nicht ihre Häufigkeitsverteilung. Die Struktur der Sprache bleibt erkennbar.

Das Problem für Verschlüsseler

Selbst mit einem Schlüsselraum von über 400 Septillionen Möglichkeiten kann ein erfahrener Kryptoanalytiker eine monoalphabetische Verschlüsselung in wenigen Minuten knacken - wenn der Geheimtext nur lang genug ist (ca. 50-100 Buchstaben).

Ausprobieren: Häufigkeitsanalyse

Häufigkeitsanalyse

Geheimtext einfügen:

Vigenère-Chiffre

Die Vigenère-Verschlüsselung wurde im 16. Jahrhundert entwickelt und galt jahrhundertelang als unknackbar - sie wurde "le chiffre indéchiffrable" (die unknackbare Verschlüsselung) genannt.

Die Lösung des Problems

Wie können wir verhindern, dass ein Buchstabe immer gleich verschlüsselt wird? Die Antwort: Wir verwenden mehrere Caesar-Verschiebungen nacheinander!

Wie funktioniert Vigenère?

Man wählt ein Schlüsselwort, z.B. "SCHLÜSSEL" → "SCHLUESSEL" (ohne Umlaute). Jeder Buchstabe des Schlüsselworts gibt an, um wie viele Stellen verschoben wird.

Beispiel:

Klartext:     H A L L O W E L T
Schlüssel:    S C H L U E S S E (wiederholt)
              │ │ │ │ │ │ │ │ │
Verschiebung: 18 2 7 11 20 4 18 18 4

Geheimtext:   Z C S W I A W D X

Das Vigenère-Quadrat:

	A	B	C	D	E	...	Z
A	A	B	C	D	E	...	Z
B	B	C	D	E	F	...	A
C	C	D	E	F	G	...	B
...	...	...	...	...	...	...	...
Z	Z	A	B	C	D	...	Y

Zeile = Schlüsselbuchstabe, Spalte = Klartextbuchstabe, Schnittpunkt = Geheimtextbuchstabe

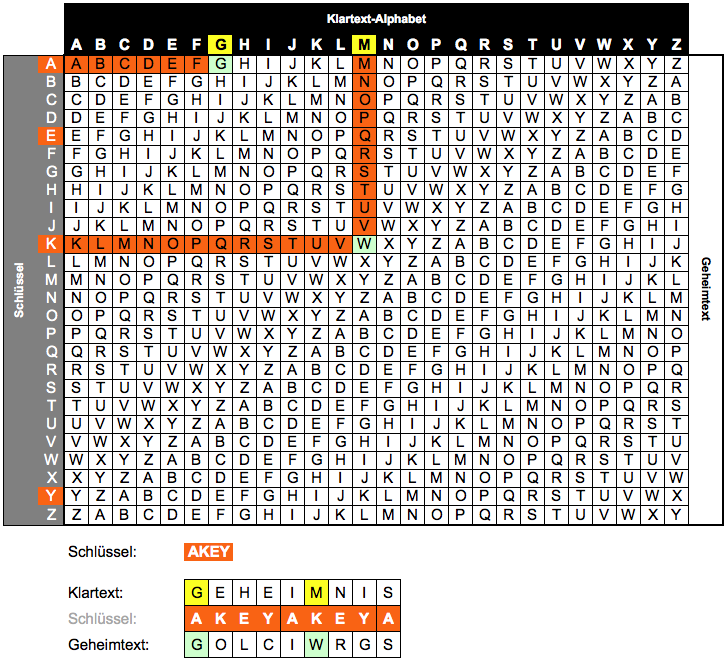
Vorteil gegenüber monoalphabetischer Substitution

Der gleiche Buchstabe wird unterschiedlich verschlüsselt! Im Beispiel wird "L" einmal zu "S" und einmal zu "W". Die Häufigkeitsanalyse funktioniert nicht mehr!

Schlüsselraum

Der Schlüsselraum der Vigenère-Verschlüsselung hängt von der Länge des Schlüsselworts ab:

• Schlüsselwort mit 1 Buchstaben: 26 Möglichkeiten (= Caesar)
• Schlüsselwort mit 2 Buchstaben: 26² = 676 Möglichkeiten
• Schlüsselwort mit 5 Buchstaben: 26⁵ ≈ 12 Millionen Möglichkeiten
• Schlüsselwort mit 10 Buchstaben: 26¹⁰ ≈ 141 Billionen Möglichkeiten

Je länger das Schlüsselwort, desto größer der Schlüsselraum und desto sicherer die Verschlüsselung!

Der Kasiski-Test: Wie man Vigenère knackt

1863 veröffentlichte Friedrich Kasiski (und unabhängig davon Charles Babbage 1854) eine Methode, um die Vigenère-Verschlüsselung zu knacken.

Schritt 1: Wiederholungen finden

Wenn sich ein Textstück im Klartext wiederholt und zufällig an der gleichen Position im Schlüsselwort steht, wiederholt sich auch der Geheimtext.

Klartext:  ... ANGRIFF ... ANGRIFF ...
Schlüssel: ... SCHLUESS... SCHLUES ...
Geheimtext:... SIUUVCX ... SIUUVCX ...
           └────────18────────┘

Schritt 2: Abstand messen

Man misst den Abstand zwischen den Wiederholungen. Im Beispiel: 18 Buchstaben.

Schritt 3: Schlüssellänge bestimmen

Der Abstand ist wahrscheinlich ein Vielfaches der Schlüssellänge. Wenn man mehrere Wiederholungen findet:

• Abstände: 18, 27, 36
• Gemeinsamer Teiler: 9
• Schlüssellänge ist wahrscheinlich 9

Schritt 4: In Gruppen aufteilen

Jetzt schreibt man den Text in Spalten mit der Breite der Schlüssellänge. Jede Spalte wurde mit dem gleichen Buchstaben des Schlüsselworts verschlüsselt - es ist also eine einfache Caesar-Verschlüsselung!

Schritt 5: Häufigkeitsanalyse auf jede Spalte

Man kann jetzt jede Spalte einzeln mit Häufigkeitsanalyse knacken, da jede Spalte nur mit einer festen Verschiebung verschlüsselt wurde.

Zusammenfassung

Die Vigenère-Verschlüsselung war ein großer Fortschritt, da sie die Häufigkeitsanalyse verhindert. Aber durch den Kasiski-Test kann man sie in ihre Einzelteile (mehrere Caesar-Verschlüsselungen) zerlegen und dann knacken.

Die Lehre: Eine sichere Verschlüsselung braucht nicht nur einen großen Schlüsselraum, sondern muss auch verhindern, dass Muster im Klartext im Geheimtext erkennbar bleiben.

---

Quiz: Antike Verschlüsselung

Teste dein Wissen über die verschiedenen Verschlüsselungsmethoden!

Antike Verschlüsselung - Wissenstest

Frage 1 von 8

Was ist der Klartext?